V torek , 15. 11. 2019, je potekala delavnica z naslovom Kako so računali v starem veku, pod vodstvom učiteljice Jane Novak Vehovar. Delavnica je bila namenjena nadarjenim in vedoželjnim učencem, večja pa je bila udeležba slednjih. Na zanimiv in drugačen način smo spoznavali, kako so računali ljudje pred nami. Spoznali smo množenje in deljenje v starem Egiptu, kitajsko grafično množenje, žaluzijo ter kronograme. Razmišljali smo, kakšni so bili ti postopki za računanje v primerjavi z današnjimi. Vsi smo se strinjali, da so si med seboj zelo različni, da so domiselni in zanimivi za reševanje. Vsekakor pa bi z njimi porabili veliko več časa, kot če uporabimo sodobne metode računanja. Med vsemi postopki računanja se nam je zdelo najtežje »staroegipčansko deljenje«. Sam postopek deljenja je precej zapleten, ampak zdelo se nam je prav osupljivo, da na koncu, kljub nenavadno pridobljenemu rezultatu, vedno dobimo pravilno rešitev.
Pri izbiri najbolj zanimivega postopka je bilo nekaterim bolj všeč »kitajsko grafično množenje«, nekaterim pa »žaluzija«. Tehniki sta si med seboj zelo različni, obe pa povezuje to, da si pri računanju ne pomagamo zgolj s tabelo, ampak postopek, s katerim pridemo do rezultata, predstavlja neke vrste umetnino.
Delavnica se nam je zdela zanimiva in drugačna. Prav gotovo bomo te postopke delili z drugimi, da jih seznanimo z računanjem v starem veku, kjer kljub enostavnemu in posplošenemu računanju dobimo pravilen rezultat.
Če želiš tudi ti preizkusiti računanje v starem veku, ti predstavljamo eno od najzanimivejših metod, in sicer »kitajsko grafično množenje«.
Izberimo si račun množenja, npr. 221 × 311
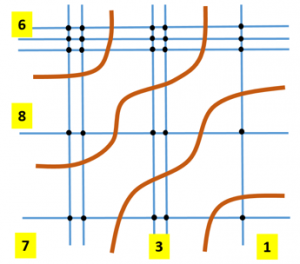
Najprej narišemo navpične črte od leve proti desni, ki prestavljajo števke prvega faktorja (2,2,1). Nato vodoravne črte drugega faktorja, od zgoraj navzdol (3,1,1). Na presečiščih označimo pike in s krivimi črtami presečišča razdelimo na 5 delov (glej sliko). Nato število pik v vsakem delu seštejemo in dobimo števila: 6, 8, 7, 3, 1. Rezultat preprosto preberemo od leve proti desni, torej 68731. To lahko tudi preverimo s kalkulatorjem in začudeni ugotovimo, da je rezultat pravilen.